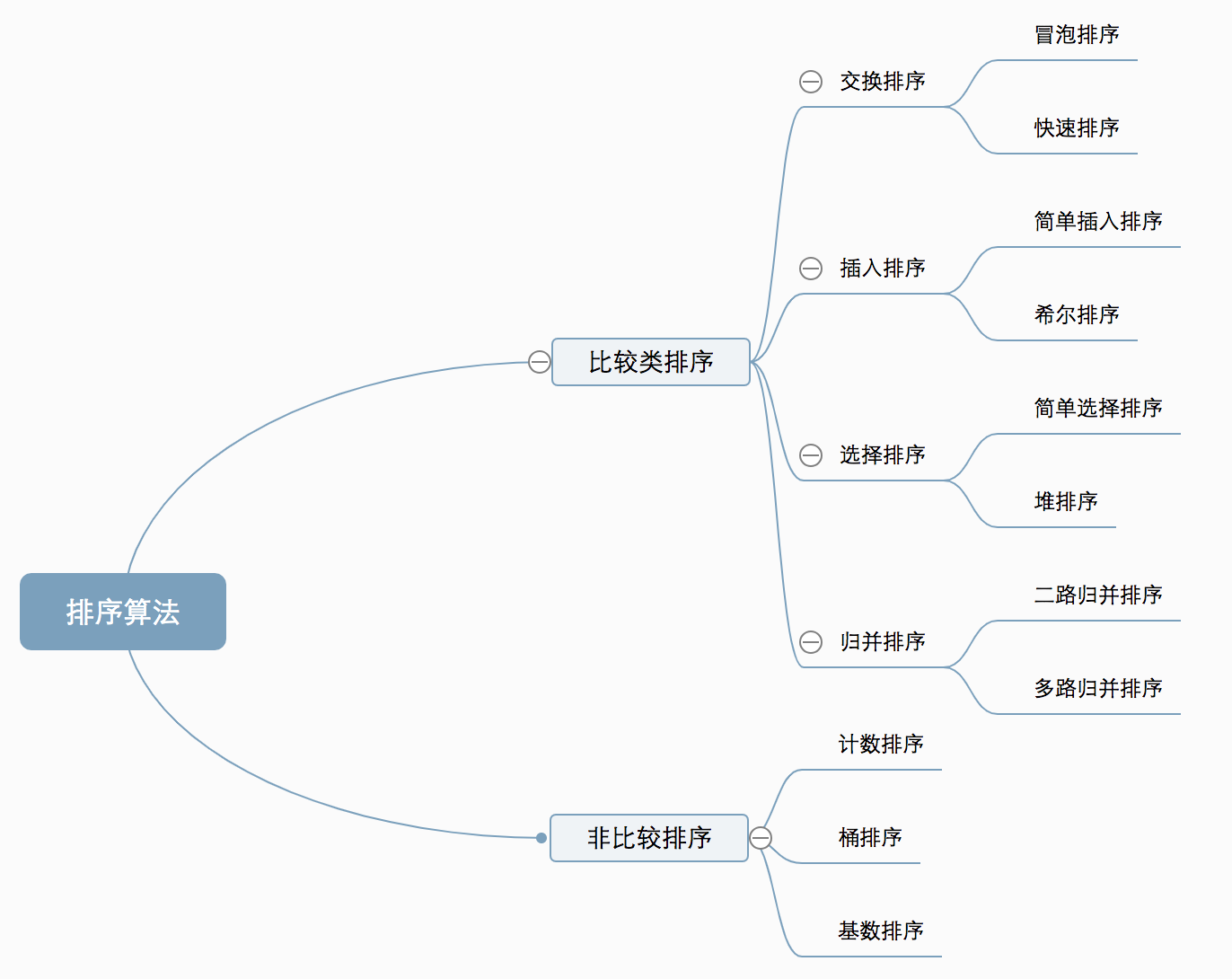
本文给出常见的十种常见排序算法的原理以及 Java 实现,按照是否比较可以分为两大类:
1、 比较类排序:通过比较来决定元素间的相对次序,由于其时间复杂度不能突破O(nlogn),因此也称为非线性时间比较类排序。
比较排序的优势是,适用于各种规模的数据,也不在乎数据的分布,都能进行排序。可以说,比较排序适用于一切需要排序的情况。
2、 非比较类排序:不通过比较来决定元素间的相对次序,它可以突破基于比较排序的时间下界,以线性时间运行,因此也称为线性时间非比较类排序。
计数排序、基数排序、桶排序则属于非比较排序。非比较排序是通过确定每个元素之前,应该有多少个元素来排序。针对数组arr,计算arr[i]之前有多少个元素,则唯一确定了arr[i]在排序后数组中的位置。
非比较排序只要确定每个元素之前的已有的元素个数即可,所有一次遍历即可解决,算法时间复杂度 O(n) 。
非比较排序时间复杂度低,但由于非比较排序需要占用空间来确定唯一位置,所以对数据规模和数据分布有一定的要求。
相关概念:
1、稳定:如果a原本在b前面,而a=b,排序之后a仍然在b的前面。
2、不稳定:如果a原本在b的前面,而a=b,排序之后 a 可能会出现在 b 的后面。
3、时间复杂度:对排序数据的总的操作次数。反映当n变化时,操作次数呈现什么规律。
4、空间复杂度:是指算法在计算机内执行时所需存储空间的度量,它也是数据规模n的函数。
冒泡排序
原理:
在要排序的一组数中,对当前还未排好序的范围内的全部数,自上而下对相邻的两个数依次进行比较和调整,让较大的数往下沉,较小的往上冒。
步骤如下:
1、从第一个数据开始,与第二个数据相比较,如果第二个数据小于第一个数据,则交换两个数据的位置。
2、指针由第一个数据移向第二个数据,第二个数据与第三个数据相比较,如果第三个数据小于第二个数据,则交换两个数据的位置。
3、依此类推,完成第一轮排序。第一轮排序结束后,最大的元素被移到了最右面。
4、依照上面的过程进行第二轮排序,将第二大的排在倒数第二的位置。
5、重复上述过程,没排完一轮,比较次数就减少一次。
代码实现:1
2
3
4
5
6
7
8
9
10
11public void bubbleSort(int[] arr) {
for(int i = 0; i < arr.length - 1; i++) {
for(int j = 0; j < arr.length - 1 - i; j++) {
if(arr[j] > arr[j+1]) {
int temp = arr[j];
arr[j] = arr[j+1];
arr[j+1] = temp;
}
}
}
}
简单选择排序
原理:
每一趟从待排序的记录中选出最小的元素,顺序放在已排好序的序列最后,直到全部记录排序完毕。
步骤如下:
1、给定数组:int[] arr={里面n个数据};
2、第1趟排序,在待排序数据arr[1]~arr[n]中选出最小的数据,将它与arr[1]交换;
3、第2趟,在待排序数据arr[2]~arr[n]中选出最小的数据,将它与arr[2]交换;
4、以此类推,第i趟在待排序数据arr[i]~arr[n]中选出最小的数据,将它与arr[i]交换,直到全部排序完成。
代码实现:1
2
3
4
5
6
7
8
9
10
11
12
13
14for(int i = 0; i < arr.length - 1; i++) {// 做第i趟排序
int k = i;
for(int j = k + 1; j < arr.length; j++){// 选最小的记录
if(arr[j] < arr[k]){
k = j; //记下目前找到的最小值所在的位置
}
}
//在内层循环结束,也就是找到本轮循环的最小的数以后,再进行交换
if(i != k){ //交换a[i]和a[k]
int temp = arr[i];
arr[i] = arr[k];
arr[k] = temp;
}
}
选择排序总结:
1、N个元素需要排序N-1轮;
2、第i轮需要比较N-i次;
3、N个元素排序,需要比较n(n-1)/2次;
4、选择排序的算法复杂度仍为O(n*n);
5、相比于冒泡排序,选择排序的交换次数大大减少,因此速度要快于冒泡排序
简单插入排序
原理:
每次执行,把后面的数插入到前面已经排序好的数组中,直到最后一个完成。
详细步骤:
利用插入法对无序数组排序时,我们其实是将数组R划分成两个子区间R[1..i-1](已排好序的有序区)和R[i..n](当前未排序的部分,可称无序区)。插入排序的基本操作是将当前无序区的第1个记录R[i]插人到有序区R[1..i-1]中适当的位置上,使R[1..i]变为新的有序区。因为这种方法每次使有序区增加1个记录,通常称增量法。
插入排序与打扑克时整理手上的牌非常类似。摸来的第1张牌无须整理,此后每次从桌上的牌(无序区)中摸最上面的1张并插入左手的牌(有序区)中正确的位置上。为了找到这个正确的位置,须自左向右(或自右向左)将摸来的牌与左手中已有的牌逐一比较。
代码实现:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21public static void InsertSort(int[] arr)
{
int i, j;
int n = arr.Length;
int target;
//假定第一个元素被放到了正确的位置上,这样,仅需遍历1 ~ n-1
for (i = 1; i < n; i++)
{
j = i;
target = arr[i];
while (j > 0 && target < arr[j - 1])
{
arr[j] = arr[j - 1];
j--;
}
arr[j] = target;
}
}
插入排序分析:
1、时间复杂度,由于仍然需要两层循环,插入排序的时间复杂度仍然为O(n*n)。
2、比较次数:在第一轮排序中,插入排序最多比较一次;在第二轮排序中插入排序最多比较二次;以此类推,最后一轮排序时,最多比较N-1次,因此插入排序的最多比较次数为1+2+…+N-1=N*(N-1)/2。尽管如此,实际上插入排序很少会真的比较这么多次,因为一旦发现左侧有比目标元素小的元素,比较就停止了,因此,插入排序平均比较次数为N*(N-1)/4。
3、移动次数:插入排序的移动次数与比较次数几乎一致,但移动的速度要比交换的速度快得多。
综上,插入排序的速度约比冒泡排序快一倍(比较次数少一倍),比选择排序还要快一些,对于基本有序的数据,插入排序的速度会很快,是简单排序中效率最高的排序算法。
快速排序
原理:
选择一个关键值作为基准值。比基准值小的都在左边序列(一般是无序的),比基准值大的都在右边(一般是无序的)。然后对这两部分分别重复这个过程,直到整个有序。
算法思想:
基于分治的思想,是冒泡排序的改进型。首先在数组中选择一个基准点(该基准点的选取可能影响快速排序的效率,后面讲解选取的方法),然后分别从数组的两端扫描数组,设两个指示标志(lo指向起始位置,hi指向末尾),首先从后半部分开始,如果发现有元素比该基准点的值小,就交换lo和hi位置的值,然后从前半部分开始扫秒,发现有元素大于基准点的值,就交换lo和hi位置的值,如此往复循环,直到lo>=hi,然后把基准点的值放到hi这个位置。一次排序就完成了。以后采用递归的方式分别对前半部分和后半部分排序,当前半部分和后半部分均有序时该数组就自然有序了。
例子:
待划分数据:7, 6, 9, 8, 5,1,假设阈值为5
第一轮:左指针指向7,右指针指向1,左指针向后移,右指针向左移,发现左面第一个大于5的元素7,右面第一个小于5的元素1,交换7和1的位置,结果:1,6,9,8,5,7;
第二轮:从6开始找大于5的数字,找到6,右边从5起找小于5的数字,找到1,但此时由于6在1的右面,,即右指针<左指针,左右指针交叉,此时划分结束。原数列被划分为两部分,左侧子数列只有一个元素,即为1,其为小于阈值的子数列;右侧子数列包括5个元素,均为大于阈值5的元素。
对于基准位置的选取一般有三种方法:固定切分,随机切分和三取样切分。固定切分的效率并不是太好,随机切分是常用的一种切分,效率比较高,最坏情况下时间复杂度有可能为O(N2).对于三数取中选择基准点是最理想的一种。
三数取中切分:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42public static int partition(int []array,int lo,int hi){
//三数取中
int mid=lo+(hi-lo)/2;
if(array[mid]>array[hi]){
swap(array[mid],array[hi]);
}
if(array[lo]>array[hi]){
swap(array[lo],array[hi]);
}
if(array[mid]>array[lo]){
swap(array[mid],array[lo]);
}
int key=array[lo];
while(lo<hi){
while(array[hi]>=key&&hi>lo){//从后半部分向前扫描
hi--;
}
array[lo]=array[hi];
while(array[lo]<=key&&hi>lo){//从前半部分向后扫描
lo++;
}
array[hi]=array[lo];
}
array[hi]=key;
return hi;
}
public static void swap(int a,int b){
int temp=a;
a=b;
b=temp;
}
public static void sort(int[] array,int lo ,int hi){
if(lo>=hi){
return ;
}
int index=partition(array,lo,hi);
sort(array,lo,index-1);
sort(array,index+1,hi);
}
分析:
1、快速排序的时间复杂度为O(NlogN).
2、快速排序在序列中元素很少时,效率将比较低,因此一般在序列中元素很少时使用插入排序,这样可以提高整体效率。
归并排序
把数据分为两段,从两段中逐个选最小的元素移入新数据段的末尾。
原理:
归并排序(Merge)是将两个(或两个以上)有序表合并成一个新的有序表。即把待排序序列分为若干个子序列,每个子序列是有序的,然后再把有序子序列合并为整体有序序列。
归并排序是建立在归并操作上的一种有效的排序算法。该算法是采用分治法(Divide and Conquer)的一个非常典型的应用。 将已有序的子序列合并,得到完全有序的序列;即先使每个子序列有序,再使子序列段间有序。若将两个有序表合并成一个有序表,称为2-路归并。
每个递归过程涉及三个步骤:
第一, 分解: 把待排序的 n 个元素的序列分解成两个子序列, 每个子序列包括 n/2 个元素.
第二, 治理: 对每个子序列分别调用归并排序MergeSort, 进行递归操作
第三, 合并: 合并两个排好序的子序列,生成排序结果.
示例如下图: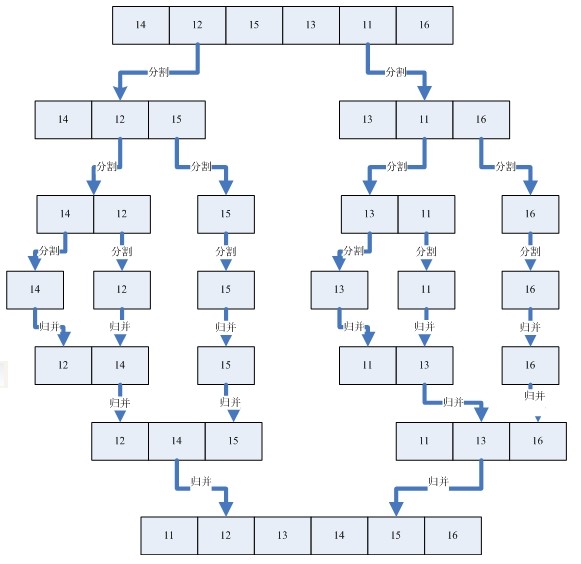
代码实现:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37public static int[] sort(int[] a,int low,int high){
int mid = (low+high)/2;
if(low<high){
sort(a,low,mid);
sort(a,mid+1,high);
//左右归并
merge(a,low,mid,high);
}
return a;
}
public static void merge(int[] a, int low, int mid, int high) {
int[] temp = new int[high-low+1];
int i= low;
int j = mid+1;
int k=0;
// 把较小的数先移到新数组中
while(i<=mid && j<=high){
if(a[i]<a[j]){
temp[k++] = a[i++];
}else{
temp[k++] = a[j++];
}
}
// 把左边剩余的数移入数组
while(i<=mid){
temp[k++] = a[i++];
}
// 把右边边剩余的数移入数组
while(j<=high){
temp[k++] = a[j++];
}
// 把新数组中的数覆盖nums数组
for(int x=0;x<temp.length;x++){
a[x+low] = temp[x];
}
}
分析:
(1)稳定性:归并排序是一种稳定的排序。
(2)存储结构要求:可用顺序存储结构。也易于在链表上实现。
(3)时间复杂度:对长度为n的文件,需进行趟二路归并,每趟归并的时间为O(n),故其时间复杂度无论是在最好情况下还是在最坏情况下均是O(nlogn)。
(4)空间复杂度:需要一个辅助向量来暂存两有序子文件归并的结果,故其辅助空间复杂度为O(n),显然它不是就地排序。
注意:若用单链表做存储结构,很容易给出就地的归并排序
希尔排序
希尔排序(Shell Sort)是插入排序的一种,是针对直接插入排序算法的改进,是将整个无序列分割成若干小的子序列分别进行插入排序,希尔排序并不稳定。该方法又称缩小增量排序,因DL.Shell于1959年提出而得名。
原理:
先取一个小于n的整数d1作为第一个增量,把文件的全部记录分成d1个组。所有距离为d1的倍数的记录放在同一个组中。先在各组内进行直接插入排序;然后,取第二个增量d2<d1重复上述的分组和排序,直至所取的增量dt=1(dt<dt-l<…<d2<d1),即所有记录放在同一组中进行直接插入排序为止。
Shell排序的执行时间依赖于增量序,好的增量序列的共同特征:
① 最后一个增量必须为1;
② 应该尽量避免序列中的值(尤其是相邻的值)互为倍数的情况。
希尔排序的时间性能优于直接插入排序的原因:
①当文件初态基本有序时直接插入排序所需的比较和移动次数均较少。
②当n值较小时,n和n2的差别也较小,即直接插入排序的最好时间复杂度O(n)和最坏时间复杂度O(n2)差别不大。
③在希尔排序开始时增量较大,分组较多,每组的记录数目少,故各组内直接插入较快,后来增量di逐渐缩小,分组数逐渐减少,而各组的记录数目逐渐增多,但由于已经按di-1作为距离排过序,使文件较接近于有序状态,所以新的一趟排序过程也较快。
因此,希尔排序在效率上较直接插人排序有较大的改进。
代码实现:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24public static void shellSort(int[] a){
double gap = a.length;//增量长度
int dk,sentinel,k;
while(true){
gap = (int)Math.ceil(gap/2);//逐渐减小增量长度
dk = (int)gap;//确定增量长度
for(int i=0;i<dk;i++){
//用增量将序列分割,分别进行直接插入排序。随着增量变小为1,最后整体进行直接插入排序
for(int j=i+dk;j<a.length;j = j+dk){
k = j-dk;
sentinel = a[j];
while(k>=0 && sentinel<a[k]){
a[k+dk] = a[k];
k = k-dk;
}
a[k+dk] = sentinel;
}
}
//当dk为1的时候,整体进行直接插入排序
if(dk==1){
break;
}
}
}
分析:
1、希尔排序的关键并不是随便分组后各自排序,而是将相隔某个“增量”的记录组成一个子序列,实现跳跃式移动,使得排序的效率提高。
2、需要注意的是,增量序列的最后一个增量值必须等于1才行。
3、由于记录是跳跃式的移动,希尔排序中相等数据可能会交换位置,所以希尔排序是不稳定的算法。
4、希尔排序最重要的地方在于当用较小步长排序后,以前用的较大步长仍然是有序的。
5、希尔排序最好时间复杂度和平均时间复杂度都是O(nlogn),最坏时间复杂度为O(n2)。
堆排序
对简单选择排序的优化。堆排序是一种树形选择排序方法,它的特点是:在排序的过程中,将array[0,…,n-1]看成是一颗完全二叉树的顺序存储结构,利用完全二叉树中双亲节点和孩子结点之间的内在关系,在当前无序区中选择关键字最大(最小)的元素。
堆的定义:
n个关键字序列array[0,…,n-1],当且仅当满足下列要求:(0 <= i <= (n-1)/2)时
① array[i] <= array[2i + 1] 且 array[i] <= array[2i + 2]; 称为小根堆;
② array[i] >= array[2i + 1] 且 array[i] >= array[2i + 2]; 称为大根堆;
步骤如下:
1、将序列构建成大顶堆。
2、将根节点与最后一个节点交换,然后断开最后一个节点。
3、重复第一、二步,直到所有节点断开。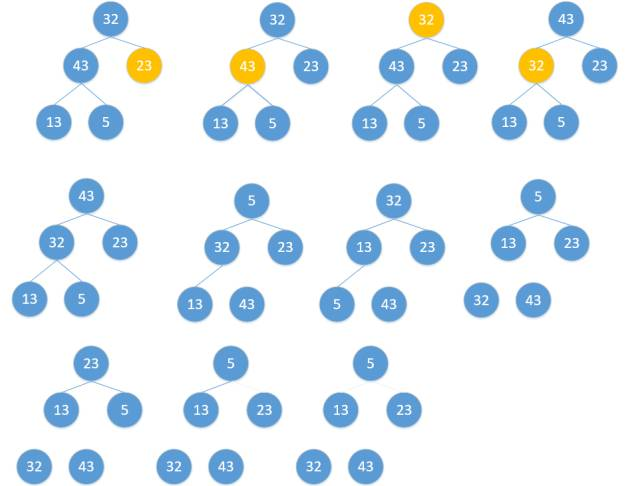
代码实现:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29/**
* 构建大顶堆
*/
public static void adjustHeap(int[] a, int i, int len) {
int temp, j;
temp = a[i];
for (j = 2 * i; j < len; j *= 2) {// 沿关键字较大的孩子结点向下筛选
if (j < len && a[j] < a[j + 1])
++j; // j为关键字中较大记录的下标
if (temp >= a[j])
break;
a[i] = a[j];
i = j;
}
a[i] = temp;
}
public static void heapSort(int[] a) {
int i;
for (i = a.length / 2 - 1; i >= 0; i--) {// 构建一个大顶堆
adjustHeap(a, i, a.length - 1);
}
for (i = a.length - 1; i >= 0; i--) {// 将堆顶记录和当前未经排序子序列的最后一个记录交换
int temp = a[0];
a[0] = a[i];
a[i] = temp;
adjustHeap(a, 0, i - 1);// 将a中前i-1个记录重新调整为大顶堆
}
}
分析:
1、空间复杂度:o(1);
2、时间复杂度:建堆:o(n),每次调整o(log n),故最好、最坏、平均情况下:o(n*logn);
3、稳定性:不稳定
计数排序
原理:
对每一个输入的元素arr[i],确定小于 arr[i] 的元素个数。
所以可以直接把 arr[i] 放到它输出数组中的位置上。假设有5个数小于 arr[i],所以 arr[i] 应该放在数组的第6个位置上。
示例如下:
需要三个数组:
待排序数组 int[] arr = new int[]{4,3,6,3,5,1};
辅助计数数组 int[] help = new int[max - min + 1]; //该数组大小为待排序数组中的最大值减最小值+1
输出数组 int[] res = new int[arr.length];
1.求出待排序数组的最大值max=6, 最小值min=1
2.实例化辅助计数数组help, help用来记录每个元素之前出现的元素个数, 此时help = [1,0,2,1,1,1]
3.计算 arr 每个数字应该在排序后数组中应该处于的位置,此时 help = [1,1,4,5,6,7];
4.根据 help 数组求得排序后的数组,此时 res = [1,3,3,4,5,6]
代码实现:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32public static int[] countSort(int[] arr){
int max = Integer.MIN_VALUE;
int min = Integer.MAX_VALUE;
//找出数组中的最大最小值
for(int i = 0; i < arr.length; i++){
max = Math.max(max, arr[i]);
min = Math.min(min, arr[i]);
}
int[] help = new int[max - min + 1];
//找出每个数字出现的次数
for(int i = 0; i < arr.length; i++){
int mapPos = arr[i] - min;
help[mapPos]++;
}
//计算每个数字应该在排序后数组中应该处于的位置
for(int i = 1; i < help.length; i++){
help[i] = help[i-1] + help[i];
}
//根据help数组进行排序
int res[] = new int[arr.length];
for(int i = 0; i < arr.length; i++){
int post = --help[arr[i] - min];
res[post] = arr[i];
}
return res;
}
分析:
1、计数排序是一种拿空间换时间的排序算法,它仅适用于数据比较集中的情况。比如 [0~100],[10000~19999] 这样的数据。
2、只能是整形数组。
3、数组元素必须都大于0。
桶排序
原理:
把数组 arr 划分为n个大小相同子区间(桶),每个子区间各自排序,最后合并 。
计数排序是桶排序的一种特殊情况,可以把计数排序当成每个桶里只有一个元素的情况。
步骤如下:
1.找出待排序数组中的最大值max、最小值min
2.我们使用 动态数组ArrayList 作为桶,桶里放的元素也用 ArrayList 存储。桶的数量为(max-min)/arr.length+1
3.遍历数组 arr,计算每个元素 arr[i] 放的桶
4.每个桶各自排序
5.遍历桶数组,把排序好的元素放进输出数组
代码实现:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35public static void bucketSort(int[] arr){
int max = Integer.MIN_VALUE;
int min = Integer.MAX_VALUE;
for(int i = 0; i < arr.length; i++){
max = Math.max(max, arr[i]);
min = Math.min(min, arr[i]);
}
//桶数
int bucketNum = (max - min) / arr.length + 1;
ArrayList<ArrayList<Integer>> bucketArr = new ArrayList<>(bucketNum);
for(int i = 0; i < bucketNum; i++){
bucketArr.add(new ArrayList<Integer>());
}
//将每个元素放入桶
for(int i = 0; i < arr.length; i++){
int num = (arr[i] - min) / (arr.length);
bucketArr.get(num).add(arr[i]);
}
//对每个桶进行排序
for(int i = 0; i < bucketArr.size(); i++){
Collections.sort(bucketArr.get(i));// 对每个桶进行排序,这里使用了Collections.sort
}
//将桶中元素全部取出来并放入 arr 中输出
int index = 0;
for (ArrayList<Integer> bucket : bucketArr) {
for (Float data : bucket) {
arr[index++] = data;
}
}
}
分析:
1、桶排序可用于最大最小值相差较大的数据情况,比如[9012,19702,39867,68957,83556,102456]。
2、但桶排序要求数据的分布必须均匀,否则可能导致数据都集中到一个桶中。比如[104,150,123,132,20000], 这种数据会导致前4个数都集中到同一个桶中。导致桶排序失效。
3、桶排序最好情况下使用线性时间O(n),桶排序的时间复杂度,取决与对各个桶之间数据进行排序的时间复杂度,因为其它部分的时间复杂度都为O(n)。很显然,桶划分的越小,各个桶之间的数据越少,排序所用的时间也会越少。但相应的空间消耗就会增大。
基数排序
基数排序(Radix Sort)分为两种:第一种是LSD ,从最低位开始排序, 第二种是 MSD 从最高位开始排。这里介绍第一种LSD排序算法。
首先,我们先了解什么是基数。基数是根据具体的排序情况而定的,比如我们常见的基数是十进制-10,还有二进制-2。
原理:
基数排序的总体思路就是将待排序数据拆分成多个关键字进行排序,也就是说,基数排序的实质是多关键字排序。通过对每一个位上的值相排序,就可以完成对整个数组的排序。
步骤如下:
1、遍历所有数组元素,找出元素最大的位值
2、从低位到高位把数组元素上的位值存入链表中
3、遍历所有链表,将链表里面的值重新赋值给数组,再清空链表。
示例如下:
例如:对数组int[ ] data = {421, 240, 35, 532, 305, 430, 124};
1、进行排序,首先我们要做的是对个位上的数值进行排序。
第一遍排序的结果为: 240 430 421 532 124 35 305
2、再进行十位上的数值排序:
第二遍排序的结果为: 305 421 124 430 532 35 240
3、再进行百位上的数值排序:
第三遍排序的结果为: 35 124 240 305 421 430 532
最后我们的到的排序结果就是: 35 124 240 305 421 430 532
代码实现:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30//实现基数排序
public void radixSort(int[] data) {
int maxBin = maxBin(data);
List<List<Integer>> list = new ArrayList<List<Integer>>();
for(int i = 0; i < 10; i ++) {
list.add(new ArrayList<Integer>());
}
for(int i = 0, factor = 1; i < maxBin; factor *= 10, i ++) {
for(int j = 0; j < data.length; j ++) {
list.get((data[j]/factor)%10).add(data[j]);
}
for(int j = 0, k = 0; j < list.size(); j ++) {
while(!list.get(j).isEmpty()) {
data[k] = list.get(j).get(0);
list.get(j).remove(0);
k ++;
}
}
}
}
//计算数组里元素的最大位数
public int maxBin(int[] data) {
int maxLen = 0;
for(int i = 0; i < data.length; i ++) {
int size = Integer.toString(data[i]).length();
maxLen = size > maxLen ? size : maxLen;
}
return maxLen;
}
算法分析:
1、基数排序基于分别排序,分别收集,所以是稳定的。但基数排序的性能比桶排序要略差,每一次关键字的桶分配都需要O(n)的时间复杂度,而且分配之后得到新的关键字序列又需要O(n)的时间复杂度。假如待排数据可以分为d个关键字,则基数排序的时间复杂度将是O(d*2n) ,当然d要远远小于n,因此基本上还是线性级别的。
2、基数排序的空间复杂度为O(n+k),其中k为桶的数量。一般来说n>>k,因此额外空间需要大概n个左右。
总结
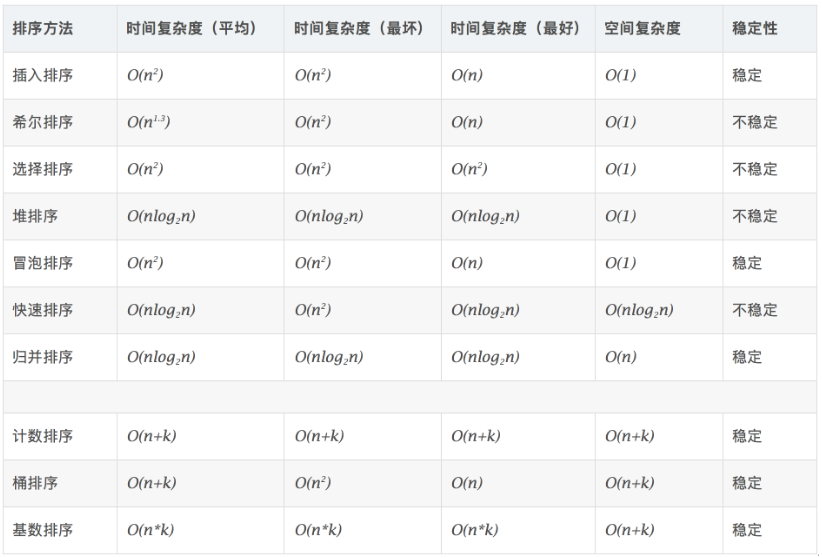
参考资料
十大经典排序算法(动图演示)
Java 排序算法分析与实现
快速排序
Java实现归并排序
Java实现希尔排序
计数排序和桶排序(Java实现)
数据结构Java版之基数排序(四)